五、计算题(每题10分,共20分) |
1、一个公牛需要测定是否为隐形杂合子,既是否是有害基因携带者,育种科学家采用86头已知携带者母牛与其交配(假设配种成功率为75%且每头母牛每次均产单犊),如果子代均为正常,我们能有多大的概率肯定该公牛不是隐形基因携带者? |
 |
答:
已知携带者母畜与待测公畜交配,若公畜为携带者,则任意一后代是正常的概率为
0.75(包括AA、Aa),则后代中全部为正常的概率P(肯定该公牛不是隐形基因携带者的概率)
P = 1 - 0.758*0.75
= 1 - 0.178
= 0.822 |
|
2、原位保种的群体遗传学基础相关计算
(1)假设某地方猪保种群,其公母比例设定为1:4,为了保证其群体有效大小达到200,若随机留种,计算公母畜分别至少需要多少。
(2)设计一个保种基础群,有公畜20头,母畜100头,若采用各家系等量留种,4个世代后群体近交系数是多少?群体有效大小?
|
 |
答:
(1)设公畜个体数为Nm,母畜个体数为Nf
Nm :Nf=1 :4 Ne=200
又由△F=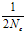 = =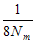 + +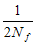
由此可计算得: Nm=62.5≈63 Nm=4·Nm=252
(2)因各家畜等量留种,所以△F=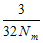 + +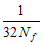 =0.005 =0.005
4个世代后群体近交系数F=1-(1-△F)4=1-(1-0.005)4≈0.02
又由公式△F=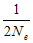 得群体有效大小Ne= 得群体有效大小Ne=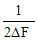 = =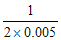 =100 =100 |
|