五、计算题(每题10分,共20分) |
1、Animal Genetics 公布了一组关于131只猫的血型数据,如下
假设血型为AA是显性纯合子,AB为杂合子,BB为阴性纯合子
请计算在这些观察到的样本中基因和基因型频率?如该群体处于Hardy-Weinbery 平衡时的基因型频率应该是多少?
基因型:AA AB BB
个体数:100 7 24 |
 |
答:
P(AA)= 100÷131=76.34%
P(AB)= 7÷131=5.34%
P(BB)= 24÷131=18.32%
假设基因A、B的频率分别为a和b,则
a= (100×2+7)÷(131×2)=79.00%
b= (24×2+7)÷(131×2)=21.00%
如果该群体处于Hardy-Weinbery 平衡,则基因型频率分别为
P(AA)= a×a =62.41%
P(AB)= 2×a×b =33.18%
P(BB)= b×b =4.41% |
|
2、对某猪群进行饲料转化率这一经济性状的选择,根据以下给出的遗传参数资料,计算其饲料转化率的遗传进展
饲料转化率的遗传力(h2)=0.35;
饲料转化率的表型标准差(σP)=0.2磅/磅(每增重1磅所需摄入的饲料磅数);
公猪选择准确度(rAIm)=0.8;
母猪选择准确度(rAIf)=0.5;
公猪选择强度(im)=-2.24;
母猪选择强度(if)=-1.554;
公猪的世代间隔(Lm)=1.8年;
母猪的世代间隔(Lf)=2.0年;
假设:饲料转化率严格服从正态分布,群体足够大满足选择需要,选择在猪群体中精确执行; |
 |
答:
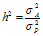 ;所以 ;所以
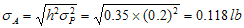
从参数资料和假设中可知:
rAIm = 0.8;rAIf = 0.5;
im=-2.42;if=-1.554;
lm=1.8;lf=-2.0;
因此:
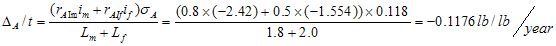
饲料转化率:家畜每增重1KG所需摄入的饲料的KG数(或者家畜每增重1磅所需摄入的饲料磅数);
因此当对于饲料转化率进行选择时,我们选择饲料转化率值低的猪留种并希望饲料转化率值是逐渐减小的;
所以我们得到遗传进展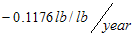 表示:猪每增重1磅所需摄入的饲料每年降低0.1176磅。 表示:猪每增重1磅所需摄入的饲料每年降低0.1176磅。 |
|