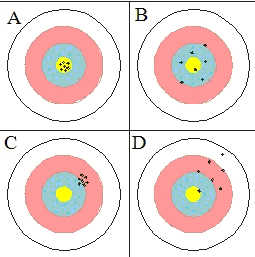
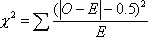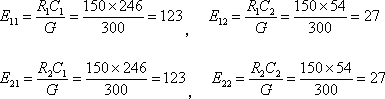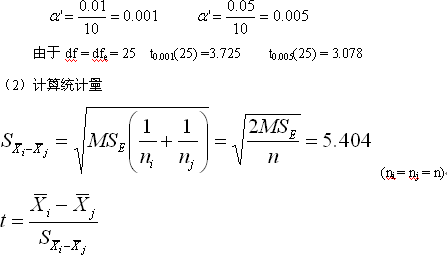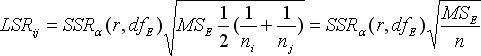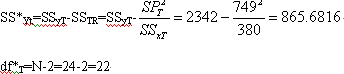四、计算题(共3题,共50分) |
1、现有5个品种的仔猪,将其置于相同的饲料和管理条件下进行饲喂,其增重如下表所示(假设每一品种代表的总体方差一致。)
分 组 |
增重 |
总 计 |
品种A |
40 |
24 |
46 |
20 |
35 |
30 |
195 |
品种B |
29 |
27 |
39 |
20 |
45 |
25 |
185 |
品种C |
41 |
61 |
47 |
67 |
69 |
40 |
325 |
品种D |
27 |
31 |
38 |
43 |
31 |
20 |
190 |
品种E |
24 |
30 |
26 |
35 |
33 |
32 |
180 |
A. 对以上数据进行方差分析。
B. 如果方差分析结果差异性显著,请用Bonferroni t 检验和Duncan’s 检验对每组均数进行多重比较。 |
 |
答:
A.
1、计算检验统计量
分 组 |
增重 |
总 计 |
均数 |
品种A |
40 |
24 |
46 |
20 |
35 |
30 |
195 |
32.5 |
品种B |
29 |
27 |
39 |
20 |
45 |
25 |
185 |
30.833 |
品种C |
41 |
61 |
47 |
67 |
69 |
40 |
325 |
54.167 |
品种D |
27 |
31 |
38 |
43 |
31 |
20 |
190 |
31.667 |
品种E |
24 |
30 |
26 |
35 |
33 |
32 |
180 |
30 |
| |
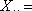 1075 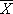 =35.833 |
2、平方和的剖分
(1)校正项:

3、自由度的剖分
(1)总自由度 dfT = nk - 1 = 29
(2)处理间自由度:dfA = k – 1= 4
(3)误差自由度:dfE = dfT – dfA = 25
4、列出方差分析表进行F检验
方差分析表
变异来源 |
平方和 |
自由度 |
均方 |
F |
处理间 |
2541.667 |
4 |
635.4168 |
7.25** |
误差项 |
2190.5 |
25 |
87.62 |
|
总 计 |
4732.167 |
29 |
|
|
查F表可知,F0.01 (4,25) = 4.18.< FA=7.25,所以可以判定至少有两个品种间仔猪的增重有极显著差异。
B.
1、Bonferroni t检验
(1)t检验次数为:c = k ( k - 1 ) = 10
当取犯I型错误概率为0.01和0.05时,每次检验的显著性水平为:
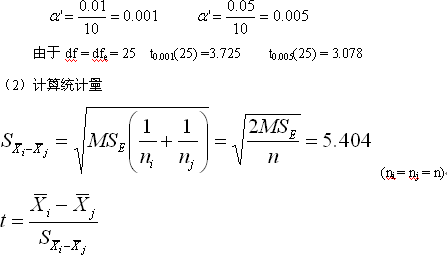
任意两组均数比较的结果如下表所示
比较 |
假设 |
t值 |
判定结果 |
H0 |
HA |
1 |
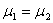
|
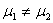
|
0.308475 |
无显著性差异 |
2 |
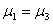
|
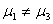
|
-4.00944 |
差异极显著 |
3 |
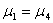
|

|
0.154145 |
无显著性差异 |
4 |
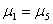
|
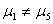
|
0.46262 |
无显著性差异 |
5 |
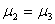
|
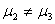
|
-4.31791 |
差异极显著 |
6 |
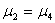
|
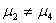
|
-0.15433 |
无显著性差异 |
7 |
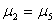
|
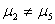
|
0.154145 |
无显著性差异 |
8 |
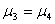
|
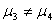
|
4.163583 |
差异极显著 |
9 |
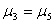
|
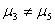
|
4.472058 |
差异极显著 |
10 |
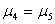
|
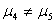
|
0.308475 |
无显著性差异 |
2、Duncan’s多重极差检验
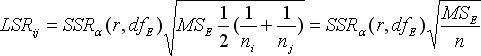
(ni = nj = n)
SSR与LSR值表
范围r SSR0.05 LSR0.05 SSR0.01 LSR0.01 |
2 2.915 11.1394 3.945 15.0754
3 3.065 11.7126 4.125 15.7633
4 3.145 12.0183 4.225 16.1454
5 3.215 12.2858 4.315 16.4893 |
Duncan’s多重极差检验结果
| 均数 |
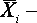 30 30 |
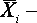 30.833 30.833 |
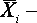 31.677 31.677 |
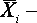 32.5 32.5 |
 =54.167 =54.167 |
24.167** |
23.334** |
22.5** |
21.667** |
 =32.5 =32.5 |
2.5ns |
1.667ns |
0.833ns |
|
 =31.667 =31.667 |
1.667ns |
0.834ns |
|
|
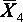 =30.833 =30.833 |
0.833ns |
|
|
|
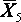 =30 =30 |
|
|
|
|
|
|
2、对下列资料进行相关和回归分析
| X |
35.0 |
45.0 |
55.0 |
65.0 |
75.0 |
| Y |
114.0 |
124.0 |
143.0 |
158.0 |
166.0 |
A. 建立方程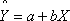
B. 求 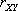
C. 检验X和Y的线性关系是否显著 |
 |
答:
A. 建立回归方程
1、计算基本统计量

C. 检验X和Y的线性关系是否显著

方差分析表
变异来源 |
平方和 |
自由度 |
均方 |
F |
回归 |
1904.4 |
1 |
1904.4 |
180.85 |
残差 |
31.6 |
3 |
10.53 |
|
总和 |
1.936 |
4 |
|
|
4、判定
因为: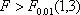 ,所以拒绝H0接受HA,即X与Y的线性关系极其显著。 ,所以拒绝H0接受HA,即X与Y的线性关系极其显著。 |
|
3、欲比较3种饲料(A1,A2,A3)对于肉牛平均日增重的影响,用24头肉牛进行了一个完全随机化试验,记录了每头牛的出生重(X)和平均日增重(Y),结果如下
饲料 |
变量 |
观测值 |
A1 |
X1
Y1 |
17 18 18 19 21 21 16 22
95 100 94 98 104 97 90 106 |
A2 |
X2
Y2 |
18 16 11 14 14 13 17 17
85 89 65 80 78 83 91 85 |
A3 |
X3
Y3 |
17 23 23 20 24 25 25 26
91 89 98 82 100 98 102 108 |
A. 如果不考虑初生重(X)的影响,对平均日增重进行单因子方差分析 (ANOVA) ,以确定不同饲料对于肉牛平均日增重的影响有无差别,不需要进行多重比较。
B. 当考虑初生重(X)的影响时,对平均日增重(Y)进行协方差分析 (ANCOVA) ,以确定不同饲料对于肉牛平均日增重的影响有无差别,不需要进行多重比较。 |
 |
答:
A.
1、提出假设:H0:3种不同饲料对肉牛平均日增重的影响没有差别。
HA:3种不同饲料对肉牛平均日增重的影响有差别。
2、计算两变量各项变异的平方和与乘积之和
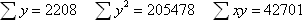
3、y变量的各项平方和
(1)y的总平方和

(4)自由度剖分
总变异 dfT=N-1=24-1=23
饲料间 dfA=m-1=3-1=2
误差 dfE=m(n-1)=3 (8-1)=21
4、对y做方差分析如下
变异来源 |
平方和 |
自由度 |
均方 |
F |
处理间 |
1216 |
2 |
608 |
11.34** |
处理内 |
1126 |
21 |
53.62 |
|
总变异 |
|
23 |
|
|
查表可知:
分析结果表明,三种饲料对增重存在极显著的差异,但由于初始体重也差异极显著,我们很难确定,是饲料还是由于初始体重对增重产生的影响,所以,我们必须进行协方差分析,以消除初始体重不同对实验结果的影响,减小实验误差,揭示出处理间真正的差异显著性。
B. 对x和 y 进行回归分析
1. 计算x的统计量

x变量的各项平方和
(1)x的总平方和

x与y的各项乘积和
(1)x与y的总乘积和

3、对回归系数作显著性检验
变异来源 |
平方和 |
自由度 |
均方 |
F |
组内项回归
组内项离回归 |
730.6532
395.3468 |
1
20 |
730.6532
19.7673 |
36.96** |
总计 |
1126 |
21 |
|
|
查表可知:  , , 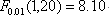
假设H0:变量y对变量x没有回归关系,HA:变量y对变量x有回归关系。
由于表中F值大于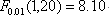 ,因此平均日增重(y)与初生重(x)有极显著的回归关系。因此应该对平均日增重(y)进行校正,以排除初生重对平均日增重的影响。说明进行协方差分析是必要的。 ,因此平均日增重(y)与初生重(x)有极显著的回归关系。因此应该对平均日增重(y)进行校正,以排除初生重对平均日增重的影响。说明进行协方差分析是必要的。
4、校正增重的方差分析
计算校正增重的各项平方和与自由度
(1)校正增重的总平方和与自由度,即校正总回归平方和及自由度。
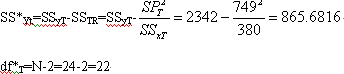
(2)校正增重的组内(误差)平方和及自由度,即组内项的离回归和及自由度

(3)校正增重的饲料组间的平方和及自由度
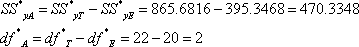
5、列出协方差分析表,进行校正值的方差分析

变异来源 |
df |
SSx |
SSy |
SPxy |
bT |
校正值变异的分析(df,SS*Y,MS,F) |
组间
组内
总计 |
2
21
23 |
256
124
380 |
1216
1126
2432 |
448
301
749 |
1.9711 |
2
20
22 |
470.3348
395.3468
865.6816 |
235.1674
19.7673 |
11.90** |
F检验结果表明,通过校正初生重影响后,各饲料间校正平均增重差异极显著,说明三种不同饲料对增重效果确有影响。 |
|