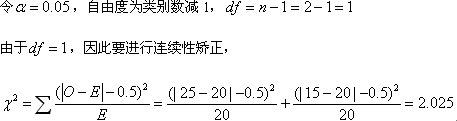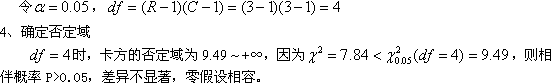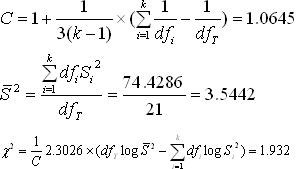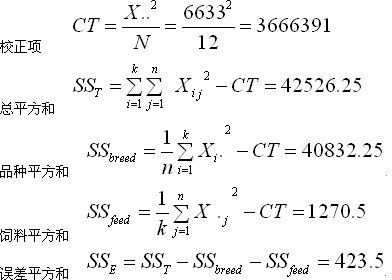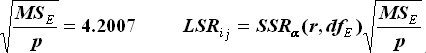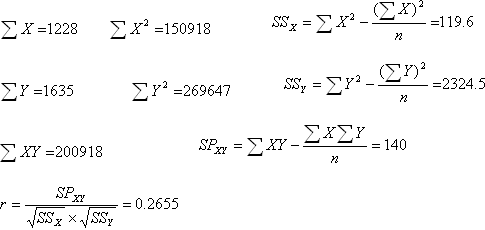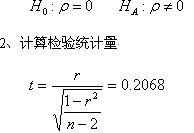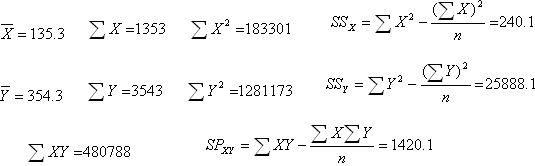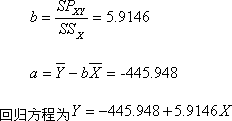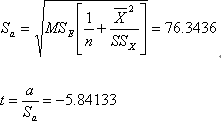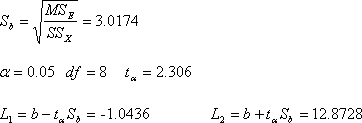四、计算题(共3题,共50分) |
1、有实验检测了断奶重仔猪,结果如下表所示,这些仔猪分别来自于3头母猪,父亲为同一头公猪。所有仔猪都在同样的条件下进行饲养,请用Bartlett检验方法对此资料的代表的3个总体方差进行同质性检验。
母猪 仔猪断奶重 总 计 |
1 24.0 22.5 24.0 20.0 22.0 23.0 22.0 22.5 180.0
2 19.0 19.5 20.0 23.5 19.0 21.0 16.5 138.5
3 16.0 16.0 15.0 20.5 14.0 17.5 15.0 15.5 19.0 148.5 |
|
 |
|
|
2、将四个猪种(A1,A2,A3、A4)用3种饲料分别饲喂3个月(每头猪只饲喂一种饲料)。实验结束后,每头猪的增重如下表所示(假设品种与饲料间没有互作)
|
饲料 |
品种 |
B1 |
B2 |
B3 |
A1 |
567 |
589 |
578 |
A2 |
622 |
633 |
644 |
A3 |
500 |
544 |
522 |
A4 |
467 |
489 |
478 |
A. 试分析品种以及饲料是否对于猪的增重有影响
B. 如果差异显著,请利用Duncan’s多重极差检验对于饲料效应进行多重比较 |
 |
答:
A.
1、提出假设
(1)对于品种效应 H0:α1=α2=α3=α4=0 HA: 至少有一个效应不为0
(2)对于饲料效应 H0:β1=β2=β3=0 HA:至少有一个效应不为0
2、计算检验统计量
|
饲料 |
总 计 平 均 |
品 种 |
B1 B2 B3 |
A1 567 589 578 1734 578
A2 622 633 644 1899 633
A3 500 544 522 1566 522
A4 467 489 478 1434 478
总计 2156 2255 2222 6633
平均 539 563.75 555.5 552.75 |
(1)平方和的剖分
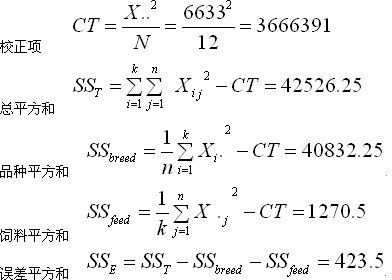
(2)自由度的剖分
总自由度 dfT = nk - 1 = 11
品种自由度 dfbreed = k – 1= 3
饲料自由度 dffeed = n – 1= 2
误差自由度 dfE = dfT – dfbreed –dffeed = 6
3、列出方差分析表进行F检验
变异来源 平方和 自由度 均方 F |
品种间 40832.25 3 13610.75 192.8323
饲料间 1270.5 2 635.25 9
误差项 423.5 6 70.58333
总 计 42526.25 11 |
4、确定显著性水平
查表可知,当显著性水平分别为0.05和0.01时,
对于品种效应:F=192.8323>F0.01(3,6)= 9.78,所以不同品种间的差异极显著,即品种的不同可以影响猪的增重。
对于饲料效应:F0.05(2,6)= 5.14<F<F0.01(2,6)=10.92,所以不同饲料间有显著性差异,即饲料的不同也可以影响猪的增重。
B.
利用Duncan’s多重极差检验对饲料效应的均值进行多重比较
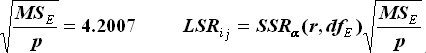
SSR与LSR值表
范围r |
SSR0.05 |
LSR0.05 |
SSR0.01 |
LSR0.01 |
2 |
3.46 |
14.53442 |
5.24 |
22.01167 |
3 |
3.58 |
15.03851 |
5.51 |
23.14586 |
Duncan’s多重极差检验结果
| 均 数 |
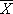 j-539 j-539 |
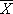 j-555.5 j-555.5 |
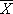 1=563.75 1=563.75 |
24.75** |
8.25ns |
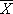 2=555.5 2=555.5 |
16.5** |
|
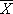 3=539 3=539 |
|
|
由多重检验结果,我们可以得知:饲料和饲料3之间有显著性差异,而饲料2和饲料1间的差异则不显著。 |
|
3、以下资料显示的是一组宁夏2岁西门塔尔公牛的体尺资料:
牛号 |
体重(kg) |
体高(cm) |
胸围(cm) |
体长(cm) |
0017 |
258 |
116 |
144 |
129 |
0013 |
407 |
127 |
176 |
132 |
0015 |
283 |
119 |
162 |
135 |
0001 |
416 |
120 |
177 |
148 |
0004 |
375 |
124 |
170 |
137 |
0011 |
363 |
125 |
127 |
136 |
0012 |
323 |
125 |
166 |
132 |
0016 |
338 |
124 |
168 |
135 |
0002 |
408 |
127 |
177 |
137 |
0009 |
372 |
121 |
168 |
132 |
A. 相关分析
a)请计算体高和胸围之间的相关系数
b)利用t检验对这两个性状间的相关性进行检验。
B. 回归分析
c)如果Y(胸围)与X(体高)线性相关,请估计回归系数,并建立回归方程。
d)检验X和Y的线性关系是否显著
e)请计算β的95%置信区间 |
 |
答:
a)
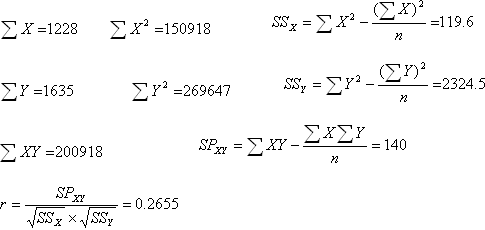
t检验
1、提出假设
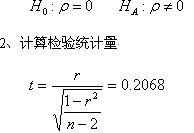
3、判定:
查表可知t0.05(df=8)=2.306>t,因此接受零假设,因此判定西门塔尔牛体高与胸围之间的相关不显著。
b)
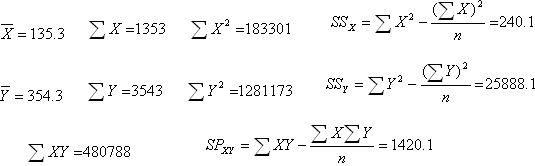
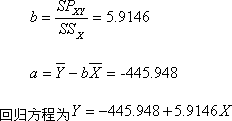
c)
对于b的检验
提出假设:H0:β=0 Ha:β≠0

方差分析表
变异来源 |
df |
SS |
MS |
F |
回归R |
1 |
8399.35 |
8399.35 |
3.8422ns |
误差E |
8 |
17488.75 |
2186.094 |
|
总和T |
9 |
25888.1 |
|
|
查表可知F=3.8422<5.32 =F0.05(1,8),因此接受原假设,认为体长对体重不存在显著的回归关系,回归方程不合适。
对于a的检验
提出假设:H0:ɑ=0 Ha:ɑ≠0
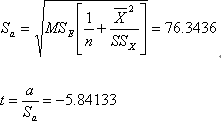
查表可知t0.05(df=8)=2.306 t0.01(df=8)=3.355<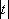 ,因此拒绝原假设,认为a不为零。 ,因此拒绝原假设,认为a不为零。
d)
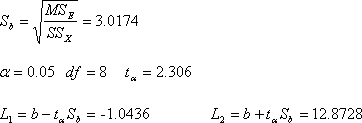
∴ β的95%的置信区间是(-1.0436,12.8728)。 |
|